कैसे भारतीय गणितज्ञों ने सुलझाई 170 साल पुरानी पहेली?

आधुनिक इतिहास के सबसे महान गणितज्ञ लेनहार्ड आयलर की अनसुलझी पहेली, जिसे लेकर वो घोषणा कर चुके थे कि इसे सुलझाना असंभव है, उस पहेली का हल दो भारतीयों ने ढूंढ निकला, जिनका नाम था आर सी बोस और शरदचंद्र श्रीखंडे.

भारतीय गणितज्ञ शरदचंद्र श्रीखंडे ने महान गणितज्ञ लेनहार्ड आयलर की अनसुलझी पहेली को सुलझा दिया(तस्वीर-Thewire/Conversation)

कमल

19 अक्तूबर 2022 (Updated: 19 अक्तूबर 2022, 20:15 IST)

Small

Medium

Large

Small

Medium

Large

"e^(i pi) = -1"

इसे दुनिया की सबसे सुन्दर इक्वेशन कहा जाता है. कारण- इस एक इक्वेशन में गणित की पांच सबसे बेसिक संख्याएं आती हैं. 0,1, पाई, i, और e. इस इक्वेशन को ईजाद करने वाले शख्स का नाम था लेनहार्ड आयलर(Leonhard Euler). जिन्हें आधुनिक इतिहास का सबसे महान गणितज्ञ माना जाता है. अपने आखिरी दिनों में आयलर की आंख की रोशनी चली गई थी. इसलिए वो बैठे -बैठे दिमाग में गणित की अबूझ पहेलियां सुलझाया करते थे. ऐसी ही एक पहेली थी जो आयलर से सुलझाए न सुलझ रही थी. आखिर में उन्होंने घोषणा करते हुए कहा कि इस पहली को सुलझाना असंभव है. 

इस घोषणा के 177 साल बाद, 26 अप्रैल 1959 को अमेरिकी अखबार न्यू यॉर्क टाइम्स (The New York Times)के मुखपत्र पर एक हेडलाइन छपी- 

“177 साल पहले लगाया गया गणित का एक अनुमान फेल हो चुका है.” 

आयलर की पहेली सुलझाई जा चुकी थी. और ऐसा करने वाले थे दो भारतीय गणितज्ञ. 
क्या थी आयलर की पहेली? 
कौन थे उसे सुलझाने वाले भारतीय गणितज्ञ?

यहां पढ़ें-जलते टैंक में बैठा रहा लेकिन पाकिस्तान को आगे बढ़ने नहीं दिया!

शुरुआत 19 अक्टूबर, 1917 से. क्या हुआ था इस रोज़? मध्यप्रदेश के सागर में एक दम्पति के यहां जन्म हुआ शरदचंद्र शंकर श्रीखंडे का(sharadchandra shankar shrikhande). उनके पिता आटा चक्की में काम करते थे. 12 लोगों का परिवार आर्थिक मुसीबत से जूझ रहा था. इसके बावजूद श्रीखंडे के पिता ने उनकी शिक्षा का इंतज़ाम किया. श्रीखंडे पढ़ने में मेधावी थे. और स्कॉलरशिप के दम पर उन्होंने नागपुर के गवर्मेंट कॉलेज ऑफ साइंस से BSC ऑनर्स में गोल्ड मैडल हासिल किया. 

नौकरी मिलना मुश्किल था. ऐसे में श्रीखंडे ने जनवरी 1940 में कलकत्ता का रुख किया. यहां उन्हें PC महालनोबिस के बनाए इंडियन स्टैटिस्टिकल इंस्टीट्यूट (ISI) में नौकरी मिल गई. ISI में श्रीखंडे की मुलाक़ात हुई राज चंद्र बोस से. जो श्रीखंडे के गुरु और रिसर्च में उनके साथी बने. दोनों ने मिलकर कोम्बीनेटरिक्स में रिर्सच शुरू की. कोम्बीनेटरिक्स यानी गणित की वो शाखा जिसमें चीजों के अलग-अलग कॉम्बिनेशंस को स्टडी किया जाता है. उदाहरण के लिए रोज़ सुबह अखबार में आने वाला सुडोकू का खेल, जो संख्याओं के कॉम्बिनेशन पर आधारित है. श्रीखंडे ने ISI में एक साल काम किया. इसके बाद वो नागपुर चले गए और वहां गणित के लेक्चरर नियुक्त हो गए. इसके बाद भी उनका राज चंद्र बोस से रिलेशन बना रहा. बोस ने श्रीखंडे को स्टैटिस्टिकल डिज़ाइन ऑफ एक्सपेरिमेंट्स नाम के एक फील्ड से रूबरू करवाया. ये क्या है? 

उदाहरण से समझिए. मान लीजिए एक किसान अपने खेत में तीन अलग उर्वरकों (फ़र्टिलाइज़र) को टेस्ट करना चाहता है. इसके लिए आम तरीका क्या होगा?
बारी-बारी से हर उर्वरक को डालकर किसान ये नतीजा निकालेगा की कौन सा उर्वरक सबसे अच्छा है. लेकिन ये तरीका एफ्फिसिएंट नहीं है. क्योंकि एक तो इसमें वक्त ज्यादा लगेगा दूसरा आप ये भी नहीं पता कर पाओगे कि जमीन के किस हिस्से पर उर्वरक ने क्या असर डाला है. संभव है कि अलग अलग नमी पर उर्वरक अलग असर देता हो.  

1920 में R.A. फिशर नाम के एक ब्रिटिश स्टैटिसटिशियन ने इसके लिए एक नया तरीका आजमाया. उन्होंने जमीन को 3 बाय 3 के हिस्सों में बांट दिया. और फिर उर्वरकों को इस तरीके से डाला कि किसी भी रो या कॉलम में कोई उर्वरक एक से ज्यादा बार न आए. फिगर 2 से आप बेहतर समझ सकते हैं. इसमें उर्वरकों को 1 से 3 की संख्या दी गई है. इस तरीके से जमीन के अलग अलग हिस्सों पर उर्वरक के असर को बेहतर स्टडी किया जा सकता है. Fisher ने जिस तरीके से उर्वरकों को डाला, उसे लैटिन स्क्वायर कहा जाता है. स्क्रीन पर दिख रहे फिगर को देखिए. किसी भी लाइन में कोई भी संख्या रिपीट नहीं हो रही होगी. लैटिन स्क्वायर का स्टैटिसिक्स में खूब इस्तेमाल होता है. इसका और बेहतर इस्तेमाल समझने के लिए एक और उदाहरण देखिए.

यहां पढ़ें-जब नेहरू के हमलावर को बचाने पहुंच गए लोहिया!

उर्वरक वाले उदाहरण में मान लीजिए अब 3 उर्वरकों के साथ साथ 3 अलग-अलग फसलें भी हैं. और आपको स्टडी करना है कि अलग-अलग जमीन के टुकड़े पर अलग-अलग फसलों पर अलग-अलग उर्वरकों का क्या असर होता है. तो इसके लिए हम एक और लैटिन स्क्वायर बना सकते हैं.  फिगर 3 में देखिए, इसमें अलग अलग फसलों को अलग-अलग रंगों से दर्शाया गया है. और किसी भी लाइन में कोई भी रंग रिपीट नहीं हो रहा. इस तरह फसलों को जमीन पर बोया गया तो ये भी लैटिन स्क्वायर बनेगा.

अब पहले उर्वरकों का जो लैटिन स्क्वायर बना था, उसे और इस स्क्वायर को मिला दीजिए, तो वो कुछ ऐसा दिखेगा (फिगर 4) इसमें हर खाने में नंबरों और रंगों का एक कॉम्बिनेशन है. लेकिन किसी भी लाइन में कोई भी कॉम्बिनेशन रिपीट नहीं हो रहा. न रंग न ही संख्या. इस तरीके में खास बात ये है कि इस तरीके से आप जमीन के एक टुकड़े पर एक समय में एक साथ 3 फसलों और 3 उर्वरकों के असर की स्टडी कर सकते हैं. इस उदाहरण में हमने दो लैटिन स्क्वायर बनाए, और उन्हें आपस में मिलाया तो वो भी लैटिन स्क्वायर ही बना. तो ऐसे लैटिन स्क्वायर्स को ओर्थोगोनल लैटिन स्क्वायर कहा जाता है. 

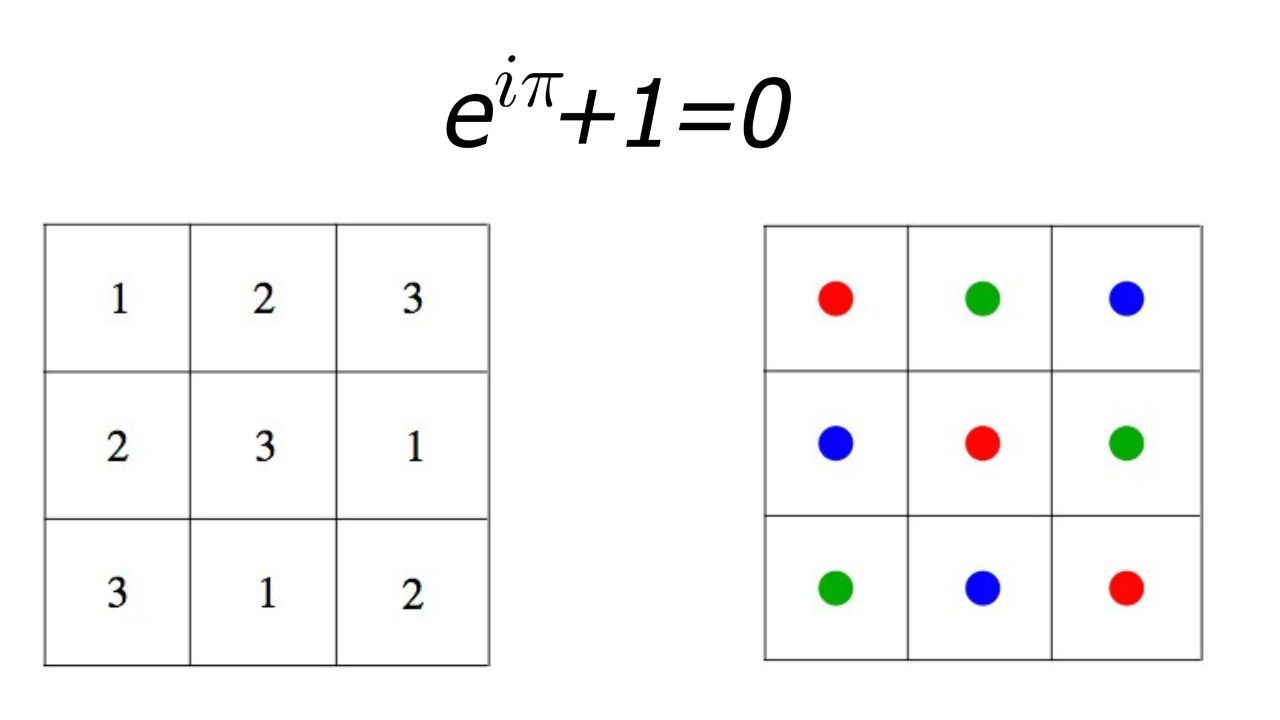
हमने जैसे दो लैटिन स्क्वायर को आपस में मिलाया, वैसे ही 3, 4, 5 स्क्वायर जोड़कर बहुत से कॉम्बिनेशन बनाए जा सकते हैं. और ये कॉम्बिनेशन ऐसे एक्सपेरिमेंट्स में काम आते हैं, जहां एक से ज्यादा वेरिएबल हो. मसलन मेडिकल रिर्सच, जहां आपको एक दवाई का परिक्षण अलग अलग उम्र वजन, लिंग, वाले मरीजों पर करना होता है.  इन्हीं लैटिन स्क्वायर से जुड़ी थी आयलर की वो पहेली, जिसके बारे में हमने आपको शुरुआत में बताया था. 

उर्वरकों वाले उदाहरण में हमने 3 बाय 3 का लैटिन स्क्वायर बनाया था. इसलिए इस स्क्वायर का आर्डर हो गया 3. आयलर ने कोशिश की कि 3 से ऊपर आर्डर के लैटिन स्क्वायर बनाए जाएं जो आपस में ओर्थोगोनल हों. यानी 4 बाय 4 , 5 बाय 5 और 6 बाय 6 के. लेकिन शर्त वही थी. किसी भी रो या कॉलम में कोई संख्या रिपीट नहीं होनी चाहिए. उसने पाया कि 6 बाय 6 के ऐसे लैटिन स्क्वायर बनाना संभव नहीं, जो आपस में ओर्थोगोनल हो. बेहतर समझने के लिए एक उदाहरण देखिए.

मान लीजिए एक मैदान में 36 आर्मी के असफर खड़े हैं. ये 36 असफर 6 अलग-अलग रेजिमेंट के हैं. यानी हर रेजिमेंट के 6 असफर. इसके अलावा एक रेजिमेंट का हर अफसर अलग-अलग लेवल का है, मसलन कर्नल, जर्नल, लेफ्टिनेंट आदि. इन 6 रेजिमेंट को हम 1 से लेकर 6 संख्यायों से दर्शा लेते हैं. और अलग-अलग पदों को रंगो से. अगर हम एक ऐसा लैटिन स्क्वायर बनाने की कोशिश करें जिसमें किसी भी लाइन में कोई भी रेजिमेंट रिपीट न हो, तो ये किया जा सकता है. (फिगर 5) एक लैटिन स्क्वायर ऐसा भी बन सकता है जिसमें एक लाइन में कोई पद रिपीट न हो. लेकिन इन दोनों को मिलाकर क्या एक ऐसा लैटिन स्क्वायर बन सकता है, जिसमें किसी भी लाइन में न रेजिमेंट रिपीट हो न लेवल. यानी किसी भी लाइन में न कुमाऊं रेजिमेंट के दो असफर होने चाहिए, न ही दो कर्नल.

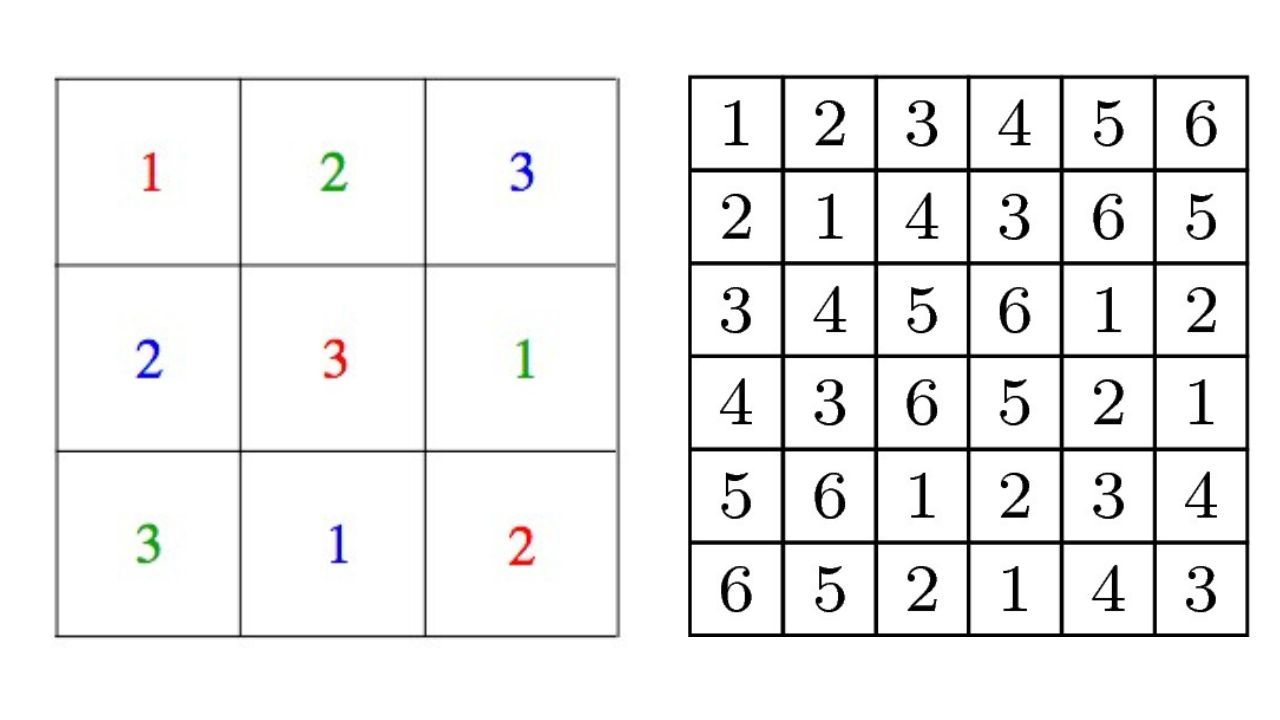
आयलर ने खूब दिमाग लगाया और वो इसका हल नहीं ढूंढ पाया. उसने घोषणा की कि ऐसा संभव ही नहीं है. और ऐसा सिर्फ 6 आर्डर के लैटिन स्क्वायर के लिए नहीं, बल्कि ऐसी कोई भी संख्या जिसे 4 से डिवाइड करने पर 2 बचता हो, उसके लिए सम्भव नहीं. मसलन 10, 14, 18, 22. यानी इन ऑर्डर्स के दो ओर्थोगोनल लैटिन स्क्वायर नहीं हो सकते. इस पहेली को तोड़ने की कई बार कोशिश हुई. साल 1901 में एक फ्रेंच गणितज्ञ गैस्टन तैरी ने प्रूव कर दिया कि ऐसा संभव ही नहीं. फिर 1959 के आसपास 3 लोगों ने इस पहेली का हल ढूंढ निकाला. ये तीन लोग थे, आर सी बोस, शरदचंद्र श्रीखंडे और ET पार्कर. 

श्रीखंडे और बोस इस दौरान यूनिवर्सिटी ऑफ नार्थ कैरोलिना में काम कर रहे थे. बोस 1949 से यहां बतौर फैकल्टी कार्यरत थे. वहीं श्रीखंडे ने 1947 में यहां अपनी PHD शुरू की थी. इत्तेफाक ये भी था कि श्रीखंडे बोस के पहले पीएचडी स्टूडेंट थे. दोनों ओर्थोगोनल लैटिन स्क्वायर की इस समस्या पर काम कर रहे थे. जब उन्हें ET पार्कर का साथ मिला. तीनों ने मिलकर इस समस्या का हल निकाला और अंत में ये प्रूव कर दिया कि  22*22 और 10 बाय 10 के ऐसे ओर्थोगोनल स्क्वायर बनाए जा सकते हैं. 1959 में तीनों ने मिलकर ये रिजल्ट अमेरिकन मैथ्स एसोसिएशन के सामने पेश किया. बोस उस दिन के बारे में याद करते हुए बताते हैं. 

“न्यू यॉर्क टाइम्स के साइंस एडिटर हमसे मिलने आए. मैं एक छोटे से होटल में रुका हुआ था. अगली सुबह जब मैं बिल चुकाने गया तो होटल के केशियर ने मेरी तरफ देखकर कहा, ‘क्या ये आपकी तस्वीर है’’

कैशियर न्यू यॉर्क टाइम्स में छपी बोस, श्रीखंडे और पार्कर की फोटो उन्हें दिखा रहा था.
बोस ने जवाब दिया हां, ये मैं ही हूं. तब कैशियर ने कहा, आपने जरूर कुछ बढ़ा काम किया होगा क्योंकि न्यू यॉर्क टाइम्स के फ्रंट पेज पर करोड़ों डॉलर देकर भी तस्वीर नहीं छपवाई जा सकती.

श्रीखंडे के बेटे मोहन तब स्कूल में पढ़ते थे. उस रोज़ उनकी टीचर ने उन्हें न्यू यॉर्क टाइम्स में उनके पिता की तस्वीर दिखाई. अखबार में 10 बाय 10 का वो लैटिन स्क्वायर भी छापा था, जिसने आयलर की बात को गलत सिद्ध साबित कर दिया था. इस खोज के बाद 1960 में श्रीखंडे भारत लौटे और तीन साल उन्होंने बनारस हिन्दू विश्विद्यालय में अपनी सेवाएं दीं. 1963 में वे बॉम्बे यूनिवर्सिटी मैथ्स डिपार्टमेंट के हेड बने और 1978 में रिटायर होने तक इस पद पर बने रहे. 1988 में अपनी पत्नी की मृत्यु के बाद वो अमेरिका अपने बच्चों के पास रहने चले गए. 2009 में भारत लौटे और अप्रैल 2020 में 102 वर्ष की उम्र में उनका निधन हो गया.